Skip to main content

Fonctions de hachage et signatures numériques

Introduction​

Après avoir exploré le chiffrement symétrique et asymétrique, abordons deux autres concepts fondamentaux de la cryptographie moderne : les fonctions de hachage et les signatures numériques.

note

Les fonctions de hachage et les signatures numériques ne servent pas à chiffrer des données (les rendre illisibles). Elles sont utilisées pour garantir l'intégrité des données, authentifier l'origine d'un message ou d'un logiciel, et assurer la non-répudiation.

Dans cette section, nous allons découvrir :

  • Ce qu'est une fonction de hachage, ses propriétés et ses utilisations.
  • Les algorithmes de hachage courants (SHA-256, SHA-3, etc.).
  • Le principe de la signature numérique et ses avantages.
  • Les algorithmes de signature numérique (RSA, DSA, ECDSA).

Préparez-vous à plonger dans des concepts un peu plus abstraits, mais essentiels pour comprendre le fonctionnement de la sécurité informatique moderne !

Commençons par les fonctions de hachage.

Propriétés des fonctions de hachage (SHA-256, SHA-3)​

Une fonction de hachage cryptographique est un algorithme qui prend en entrée une donnée de taille variable (un message, un fichier, etc.) et produit en sortie une empreinte numérique de taille fixe, appelée hash.

Propriétés fondamentales​

Une bonne fonction de hachage cryptographique doit posséder les propriétés suivantes :

  1. Déterministe : Pour une même entrée, la fonction doit toujours produire le même hash.
  2. Calcul rapide : La fonction doit être rapide à calculer, même pour de grandes entrées.
  3. Taille fixe : Le hash doit avoir une taille fixe, quelle que soit la taille de l'entrée (par exemple, 256 bits pour SHA-256).
  4. Effet avalanche : Une petite modification de l'entrée (par exemple, changer un seul bit) doit entraîner une modification importante du hash (idéalement, la moitié des bits du hash doivent changer).
  5. Résistance à la pré-image : Étant donné un hash h, il doit être computationnellement infaisable de trouver une entrée m.
  6. Résistance aux collisions : Il doit être computationnellement infaisable de trouver deux entrées différentes m1 et m2 telles que hash(m1) = hash(m2).
info

Ces propriétés garantissent que :

  • Le hash est une représentation unique (ou presque) de l'entrée.
  • Il est impossible (en pratique) de retrouver l'entrée à partir du hash.
  • Il est impossible (en pratique) de modifier l'entrée sans modifier le hash.
  • Il est impossible (en pratique) de trouver deux entrées différentes qui produisent le même hash.

Utilisations des fonctions de hachage​

  • Vérification de l'intégrité des données : Si le hash d'un fichier téléchargé correspond au hash fourni par la source, on peut être sûr que le fichier n'a pas été modifié pendant le téléchargement.
  • Stockage sécurisé des mots de passe : Au lieu de stocker les mots de passe en clair, on stocke leur hash (éventuellement combiné avec un sel). Cela empêche un attaquant de lire les mots de passe s'il accède à la base de données.
  • Signature numérique : On signe le hash d'un document plutôt que le document lui-même, ce qui est plus efficace (nous y reviendrons).
  • Cryptomonnaies : Les fonctions de hachage sont utilisées pour sécuriser les transactions et créer des blocs dans la blockchain.
  • Détection de logiciels malveillants : Les antivirus comparent le hash des fichiers à une base de données de hashs de malwares connus.
  • Indexation de données : Les fonctions de hachage peuvent être utilisées pour indexer rapidement des données dans une table de hachage.

Algorithmes de hachage courants​

MD5 (Message Digest 5)​

  • Développé par : Ron Rivest (1991).
  • Taille du hash : 128 bits.
  • Sécurité : MD5 est aujourd'hui considéré comme cassé. Des collisions ont été trouvées, ce qui signifie qu'il est possible de créer deux fichiers différents avec le même hash MD5.
Ne plus utiliser MD5 !

MD5 ne doit plus être utilisé pour des applications de sécurité.

SHA-1 (Secure Hash Algorithm 1)​

  • Développé par : La NSA (1995).
  • Taille du hash : 160 bits.
  • Sécurité : SHA-1 est aujourd'hui considéré comme faible. Des collisions ont été trouvées, et il est recommandé de ne plus l'utiliser.
Éviter SHA-1

SHA-1 est en voie d'obsolescence. Il est préférable d'utiliser des algorithmes plus récents.

SHA-2​

SHA-2 est une famille de fonctions de hachage développée par la NSA. Elle comprend plusieurs variantes :

  • SHA-256 : hash de 256 bits (description détaillée plus loin).

  • SHA-384 : hash de 384 bits.

  • SHA-512 : hash de 512 bits.

  • Sécurité : SHA-2 est actuellement considéré comme sûr. Il est largement utilisé.

SHA-3​

SHA-3 est le dernier né des standards de fonctions de hachage, sélectionné par le NIST en 2012 (à la suite d'une compétition publique).

  • Développé par : Guido Bertoni, Joan Daemen, Michaël Peeters et Gilles Van Assche.
  • Principe : SHA-3 utilise une construction appelée "éponge" (sponge construction), qui est différente de celle de MD5, SHA-1 et SHA-2.
  • Variantes : SHA3-224, SHA3-256, SHA3-384, SHA3-512 (les nombres indiquent la taille du hash en bits).
  • Sécurité : SHA-3 est considéré comme très sûr. Il offre une alternative à SHA-2 en cas de découverte de faiblesses dans cette famille.
tip

SHA-256 et SHA-3 sont les algorithmes de hachage à privilégier aujourd'hui. Ils offrent un bon niveau de sécurité et sont largement supportés.

SHA-256 (Secure Hash Algorithm 256 bits)​

SHA-256 est une fonction de hachage cryptographique qui produit un haché de 256 bits (32 octets), quelle que soit la taille de l'entrée. C'est l'un des algorithmes de hachage les plus utilisés aujourd'hui.

Fonctionnement interne (simplifié) de SHA-256​

SHA-256, comme les autres membres de la famille SHA-2, est basé sur la construction de Merkle-Damgård. Voici les étapes principales :

  1. Prétraitement (padding) :

    • Le message d'entrée (qui peut être de n'importe quelle taille) est d'abord "rembourré" (padded) pour que sa longueur (en bits) soit un multiple de 512 bits.
    • Le rembourrage consiste à ajouter :
      • Un bit '1'.
      • Un certain nombre de bits '0'.
      • La longueur du message original (avant rembourrage), codée sur 64 bits.

  2. Initialisation :

    • Huit variables de hachage (h0h_0 à h7h_7) de 32 bits chacune sont initialisées avec des valeurs constantes spécifiques. Ces valeurs sont dérivées des racines carrées des huit premiers nombres premiers.

  3. Traitement par blocs :

    • Le message rembourré est divisé en blocs de 512 bits.
    • Chaque bloc est traité séquentiellement, en mettant à jour les variables de hachage.

  4. Fonction de compression :

    • C'est le cœur de l'algorithme. Elle prend en entrée :

      • Le bloc de message de 512 bits courant.
      • Les huit variables de hachage (256 bits au total) issues du bloc précédent (ou les valeurs initiales pour le premier bloc).

    • Elle produit en sortie :

      • Huit nouvelles variables de hachage (256 bits au total).

    • La fonction de compression effectue 64 tours de calculs, en utilisant :

      • Des opérations logiques (ET, OU, XOR, NON).
      • Des rotations de bits.
      • Des additions modulaires (modulo 2322^{32}).
      • Six constantes logiques.
      • 64 constantes de tour (KtK_t), dérivées des parties fractionnaires des racines cubiques des 64 premiers nombres premiers.
      • Un "message schedule" qui dérive 64 mots de 32 bits (WtW_t) à partir du bloc de message de 512 bits.

  5. Sortie :

    • Après le traitement du dernier bloc, les huit variables de hachage finales (h0h_0 à h7h_7) sont concaténées pour former le haché de 256 bits.

Exemple (Python)​

import hashlib

# Message à hacher
message = b"Ceci est un message a hacher."

# Calcul du hash SHA-256
sha256_hash = hashlib.sha256(message).hexdigest()
print(f"SHA-256 : {sha256_hash}")

# Calcul du hash SHA-3 (256 bits)
sha3_256_hash = hashlib.sha3_256(message).hexdigest()
print(f"SHA3-256 : {sha3_256_hash}")

Intégrité des données​

L'une des principales applications des fonctions de hachage cryptographiques est la vérification de l'intégrité des données. En calculant le hash d'un fichier (ou d'un message) et en le comparant à un hash de référence, on peut s'assurer que le fichier n'a pas été modifié, que ce soit accidentellement ou intentionnellement.

Principe​

  1. Calcul du hash : Le propriétaire d'un fichier (ou l'expéditeur d'un message) calcule le hash du fichier à l'aide d'une fonction de hachage cryptographique (par exemple, SHA-256).
  2. Publication du hash : Le hash est publié ou transmis avec le fichier (par exemple, sur une page web de téléchargement, dans un email, etc.).
  3. Vérification du hash : Le destinataire du fichier (ou le téléchargeur) recalcule le hash du fichier reçu avec la même fonction de hachage.
  4. Comparaison : Le hash calculé est comparé au hash de référence.
    • Si les hashs sont identiques : Le fichier est intègre (il n'a pas été modifié).
    • Si les hashs sont différents : Le fichier a été modifié (corrompu, altéré, infecté par un malware, etc.).
Schéma

Exemples d'utilisation​

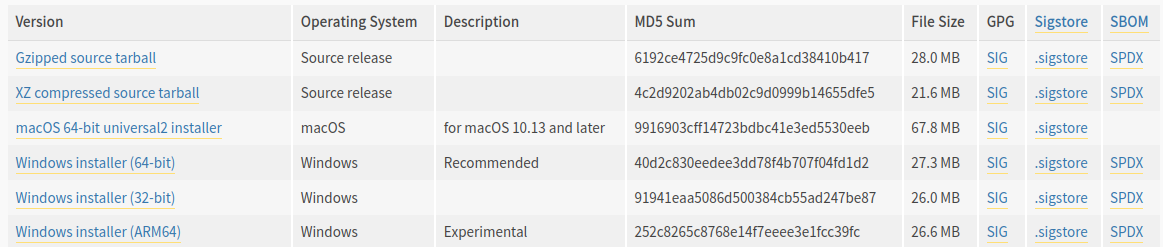
  • Téléchargement de logiciels : De nombreux sites web qui proposent des logiciels en téléchargement fournissent également le hash (MD5, SHA-1 ou SHA-256) des fichiers. Cela permet aux utilisateurs de vérifier que le fichier téléchargé n'a pas été corrompu pendant le transfert ou modifié par un tiers (par exemple, en y injectant un malware).

  • Intégrité des emails : Certains systèmes de messagerie utilisent des fonctions de hachage pour vérifier l'intégrité des pièces jointes.

  • Intégrité des systèmes de fichiers : Des outils comme AIDE (Advanced Intrusion Detection Environment) ou Tripwire utilisent des fonctions de hachage pour détecter les modifications non autorisées des fichiers système.

  • Intégrité des sauvegardes : Les fonctions de hachage peuvent être utilisées pour vérifier que les sauvegardes n'ont pas été corrompues.

Limites​

  • Attaque de l'homme du milieu (MitM) : Si un attaquant parvient à intercepter la communication entre l'expéditeur et le destinataire, il peut modifier le fichier et le hash de référence. Dans ce cas, la vérification du hash ne détectera pas la modification. C'est pourquoi il est important d'utiliser des canaux de communication sécurisés (HTTPS, etc.) pour télécharger des fichiers ou échanger des hashs.
  • Fonctions de hachage faibles : Si une fonction de hachage faible (comme MD5 ou SHA-1) est utilisée, un attaquant peut être en mesure de créer un fichier différent avec le même hash (collision), ce qui lui permettrait de faire passer un fichier malveillant pour un fichier légitime.
tip

Pour garantir l'intégrité des données, il est essentiel d'utiliser des fonctions de hachage cryptographiques fortes (comme SHA-256 ou SHA-3) et de protéger le hash de référence contre les modifications non autorisées (par exemple, en le publiant sur un site web sécurisé avec HTTPS).

Signature numérique et authentification​

La signature numérique est un mécanisme cryptographique qui permet de garantir l'intégrité d'un document (ou d'un message, d'un logiciel, etc.) et d'authentifier son auteur. Elle est l'équivalent numérique d'une signature manuscrite.

note

La signature numérique repose sur la cryptographie à clé publique (asymétrique).

Principe de base​

  1. Calcul du hash : L'auteur du document calcule le hash du document à l'aide d'une fonction de hachage cryptographique.
  2. Chiffrement du hash : L'auteur chiffre le hash avec sa clé privée. Ce hash chiffré constitue la signature numérique.
  3. Attachement de la signature : La signature numérique est attachée au document (ou envoyée séparément).
  4. Vérification de la signature : Le destinataire du document :
    • Calcule le hash du document reçu avec la même fonction de hachage que l'auteur.
    • Déchiffre la signature numérique avec la clé publique de l'auteur.
    • Compare le hash calculé et le hash déchiffré.
      • Si les hashs sont identiques : La signature est valide. Cela signifie que :
        • Le document n'a pas été modifié depuis qu'il a été signé (intégrité).
        • Le signataire est bien celui qu'il prétend être (authentification), car seule la clé privée de l'auteur peut produire une signature qui se déchiffre correctement avec sa clé publique.
      • Si les hashs sont différents : La signature n'est pas valide. Le document a été modifié, ou la signature ne provient pas de l'auteur présumé.

Avantages de la signature numérique​

  • Intégrité : Garantit que le document n'a pas été modifié depuis qu'il a été signé.
  • Authentification : Permet de vérifier l'identité du signataire.
  • Non-répudiation : Le signataire ne peut pas nier avoir signé le document (sauf si sa clé privée a été compromise).

Algorithmes de signature numérique​

Plusieurs algorithmes de signature numérique existent, basés sur différents problèmes mathématiques :

  • RSA : On peut utiliser l'algorithme RSA "à l'envers" pour signer : au lieu de chiffrer avec la clé publique et de déchiffrer avec la clé privée, on "chiffre" le hash avec la clé privée et on "déchiffre" avec la clé publique. En pratique, on utilise des schémas de signature spécifiques basés sur RSA, comme PKCS#1 v1.5 ou PSS (Probabilistic Signature Scheme).
  • DSA (Digital Signature Algorithm) : Un algorithme spécifiquement conçu pour la signature numérique, basé sur le problème du logarithme discret.
  • ECDSA (Elliptic Curve Digital Signature Algorithm) : Une variante de DSA qui utilise les courbes elliptiques. ECDSA est de plus en plus utilisé, car il offre une meilleure sécurité pour une taille de clé donnée que RSA ou DSA.

Utilisations de la signature numérique​

  • Signature de documents électroniques : Contrats, factures, etc.
  • Authentification de logiciels : Les éditeurs de logiciels signent numériquement leurs logiciels pour permettre aux utilisateurs de vérifier leur authenticité et leur intégrité.
  • Sécurisation des transactions en ligne : Les signatures numériques sont utilisées dans les protocoles de paiement en ligne (par exemple, SET, Secure Electronic Transaction).
  • Certificats numériques : Les autorités de certification utilisent des signatures numériques pour signer les certificats numériques.
  • Cryptomonnaies : Les transactions en cryptomonnaies sont signées numériquement par les utilisateurs.
  • Sécurisation des mises à jour logicielles : Les mises à jour logicielles sont souvent signées numériquement par l'éditeur pour éviter qu'un attaquant ne distribue une mise à jour malveillante.

Exemple (Python)​

from cryptography.hazmat.primitives import hashes
from cryptography.hazmat.primitives.asymmetric import padding
from cryptography.hazmat.primitives.asymmetric import rsa
from cryptography.exceptions import InvalidSignature

# Génération d'une paire de clés RSA (pour l'exemple)
private_key = rsa.generate_private_key(
    public_exponent=65537,
    key_size=2048
)
public_key = private_key.public_key()

# Message à signer
message = b"Ceci est un message a signer."

# Signature du message avec la clé privée
signature = private_key.sign(
    message,
    padding.PSS(
        mgf=padding.MGF1(hashes.SHA256()),
        salt_length=padding.PSS.MAX_LENGTH
    ),
    hashes.SHA256()
)
print(f"Signature : {signature.hex()}")

# Vérification de la signature avec la clé publique
try:
    public_key.verify(
        signature,
        message,
        padding.PSS(
            mgf=padding.MGF1(hashes.SHA256()),
            salt_length=padding.PSS.MAX_LENGTH
        ),
        hashes.SHA256()
    )
    print("La signature est valide.")
except InvalidSignature:
    print("La signature est invalide !")

# Test avec un message modifié
modified_message = b"Ceci est un message modifie."
try:
    public_key.verify(
        signature,
        modified_message,  # Message modifié !
        padding.PSS(
            mgf=padding.MGF1(hashes.SHA256()),
            salt_length=padding.PSS.MAX_LENGTH
        ),
        hashes.SHA256()
    )
    print("La signature est valide.")
except InvalidSignature:
    print("La signature est invalide (comme attendu) !")
info

Dans cet exemple :

  • On utilise la bibliothèque cryptography pour générer une paire de clés RSA, signer un message avec la clé privée et vérifier la signature avec la clé publique.
  • On utilise le schéma de signature PSS (Probabilistic Signature Scheme) avec RSA, qui est recommandé pour la sécurité.
  • On utilise SHA-256 comme fonction de hachage.
  • On montre comment la vérification de la signature échoue si le message est modifié.
tip

La signature numérique est un outil puissant pour garantir l'intégrité et l'authenticité des données numériques. Elle est au cœur de nombreux protocoles de sécurité et applications modernes.

Exemple : OpenPGP (Pretty Good Privacy)​

OpenPGP (Pretty Good Privacy) est un standard de chiffrement et d'authentification de données, souvent utilisé pour sécuriser les emails, mais aussi pour chiffrer des fichiers, des partitions de disque, etc. Il est basé sur le logiciel PGP, créé par Phil Zimmermann en 1991.

note

OpenPGP est un standard ouvert, décrit dans la RFC 4880. Il existe plusieurs implémentations d'OpenPGP, la plus connue étant GnuPG (GNU Privacy Guard, ou GPG).

Fonctionnalités d'OpenPGP​

  • Chiffrement hybride : OpenPGP utilise à la fois le chiffrement asymétrique (pour l'échange de clés) et le chiffrement symétrique (pour le chiffrement des données).
  • Signature numérique : OpenPGP permet de signer numériquement les messages et les fichiers, garantissant ainsi leur intégrité et l'authenticité de l'expéditeur.
  • Gestion des clés : OpenPGP utilise un système de trousseau de clés (keyring) pour stocker les clés publiques et privées.
  • Toile de confiance (web of trust) : OpenPGP propose un modèle de confiance décentralisé, où les utilisateurs peuvent signer les clés publiques des autres pour attester de leur confiance en l'identité de ces personnes (contrairement au modèle centralisé des PKI, basé sur les autorités de certification).

Scénario typique (envoi d'un email chiffré et signé)​

Voici comment Alice peut envoyer un email chiffré et signé à Bob en utilisant OpenPGP :

  1. Alice et Bob génèrent leurs paires de clés :

    • Chacun génère une paire de clés OpenPGP (clé publique et clé privée).
    • Ils conservent précieusement leur clé privée.
    • Ils peuvent diffuser leur clé publique (par exemple, sur un serveur de clés, sur leur site web, etc.).

  2. Alice obtient la clé publique de Bob :

    • Alice récupère la clé publique de Bob (par exemple, à partir d'un serveur de clés, d'un email précédent de Bob, etc.).

  3. Alice rédige son email.

  4. Alice signe l'email :

    • GPG calcule le hash de l'email.
    • GPG chiffre le hash avec la clé privée d'Alice. C'est la signature numérique.

  5. Alice chiffre l'email (et la signature) :

    • GPG génère une clé de session aléatoire (pour un algorithme de chiffrement symétrique, comme AES).
    • GPG chiffre l'email (et la signature) avec cette clé de session.
    • GPG chiffre la clé de session avec la clé publique de Bob.

  6. Alice envoie l'email chiffré et signé à Bob.

  7. Bob reçoit l'email.

  8. Bob déchiffre l'email :

    • GPG utilise la clé privée de Bob pour déchiffrer la clé de session.
    • GPG utilise la clé de session pour déchiffrer l'email (et la signature).

  9. Bob vérifie la signature :

    • GPG calcule le hash de l'email reçu.
    • GPG déchiffre la signature avec la clé publique d'Alice.
    • GPG compare les deux hashs. Si les hashs sont identiques, la signature est valide (l'email est intègre et provient bien d'Alice).

Outils OpenPGP​

  • GnuPG (GPG) : L'implémentation GNU de OpenPGP, en ligne de commande. C'est l'outil de base.
  • Clients email avec support OpenPGP : Thunderbird, Mailvelope, Gpg4win.
  • Applications graphiques : Kleopatra (KDE), GPA (GNU Privacy Assistant), Seahorse (GNOME), etc.

Très bien, voici une proposition pour remplacer l'exemple théorique d'OpenPGP par un tutoriel pratique utilisant Gpg4win sous Windows, incluant la vérification de l'intégrité du logiciel téléchargé :

Exemple : Utilisation de Gpg4win (OpenPGP sous Windows)​

Gpg4win (GNU Privacy Guard for Windows) est une suite logicielle gratuite qui permet d'utiliser OpenPGP sous Windows. Elle inclut :

  • GnuPG (GPG) : Le moteur de chiffrement et de signature (en ligne de commande).
  • Kleopatra : Une interface graphique pour gérer les clés et les certificats.
  • GPA (GNU Privacy Assistant) : Une autre interface graphique pour gérer les clés.
  • GpgOL : Un plugin pour Microsoft Outlook (chiffrement et signature des emails).
  • GpgEX : Une extension pour l'Explorateur Windows (chiffrement et signature de fichiers).

1. Téléchargement et vérification de Gpg4win​

  1. Téléchargement :

  2. Vérification de l'intégrité (SHA-256) :

    • Pourquoi vérifier ? Il est essentiel de vérifier l'intégrité du fichier téléchargé pour s'assurer qu'il n'a pas été modifié (par exemple, par un attaquant qui aurait injecté un malware).

    • Méthode (PowerShell) :

      1. Ouvrez PowerShell (tapez "PowerShell" dans la barre de recherche Windows).
      2. Naviguez jusqu'au répertoire où vous avez téléchargé le fichier gpg4win-*.exe (en utilisant la commande cd). Par exemple : 
        cd C:\Users\VotreNom\Downloads
      3. Calculez le haché SHA-256 du fichier : 
        Get-FileHash .\gpg4win-*.exe -Algorithm SHA256
        (Remplacez gpg4win-*.exe par le nom exact du fichier téléchargé.)
      4. Comparez le haché affiché par PowerShell avec le haché SHA-256 fourni sur le site de Gpg4win (et recopié ici pour plus de commodité) : 
        765673854c1503602b09c97bfa6c72b534e2414185fb2f23a0ce19cf8cecd891
        Si les deux hachés sont identiques, le fichier est intègre. Si les hachés sont différents, ne l'installez pas !

    • Méthode alternative (ligne de commande) :

      certutil -hashfile  .\gpg4win-*.exe SHA256

2. Installation de Gpg4win​

  1. Exécutez le fichier gpg4win-*.exe téléchargé.
  2. Suivez les instructions de l'installateur. Vous pouvez laisser les options par défaut (sauf si vous avez des besoins spécifiques).

3. Génération d'une paire de clés​

  1. Ouvrez Kleopatra :
    • Kleopatra est l'interface graphique principale de Gpg4win pour la gestion des clés. Vous la trouverez dans le menu Démarrer.
  2. Créez une nouvelle paire de clés :
    • Cliquez sur "Fichier" -> "NCréer une paire de clés OpenPGP personnelle".
    • Entrez votre nom et votre adresse email (ces informations seront associées à votre clé).
    • Cliquez sur "Paramètres avancés...".
      • Vous pouvez choisir l'algorithme de chiffrement (RSA est recommandé) et la taille de la clé (4096 bits est une bonne pratique actuelle).
    • Cliquez sur "OK", puis sur "Créer".
    • Choisissez un mot de passe (une passphrase) fort pour protéger votre clé privée. Notez-le précieusement et ne l'oubliez pas ! Sans ce mot de passe, votre clé privée sera inutilisable.
    • Gpg4win génère votre paire de clés. Cela peut prendre quelques instants.

4. Exportation de votre clé publique​

  1. Sélectionnez votre clé :
    • Dans Kleopatra, votre clé nouvellement créée devrait apparaître dans la liste.
  2. Exportez votre clé publique :
    • Faites un clic droit sur votre clé et choisissez "Exporter...".
    • Enregistrez le fichier (par exemple, cle_publique.asc). Ce fichier contient votre clé publique, que vous pourrez partager avec d'autres personnes.

5. Importation d'une clé publique​

  1. Obtenez la clé publique de votre correspondant :
    • Votre correspondant doit vous envoyer sa clé publique (par exemple, par email, via un serveur de clés, etc.).
  2. Importez la clé publique :
    • Dans Kleopatra, cliquez sur "Importer...".
    • Sélectionnez le fichier contenant la clé publique de votre correspondant.
    • Kleopatra importe la clé et l'ajoute à votre trousseau.

6. Chiffrement d'un fichier pour votre correspondant​

  1. Sélectionnez le fichier :
    • Dans l'Explorateur Windows, faites un clic droit sur le fichier que vous souhaitez chiffrer.
  2. Chiffrez le fichier :
    • Dans le menu contextuel, choisissez "Signer et chiffrer".
    • Dans la fenêtre qui s'ouvre, sélectionnez "Chiffrer".
    • Choisissez le(s) destinataire(s) : cochez la case correspondant à la clé publique de votre/vos destinataire(s). (Vous pouvez aussi vous ajouter vous-même comme destinataire pour pouvoir déchiffrer le fichier).
    • Cliquez sur "Suivant" puis "Chiffrer".
    • Gpg4win crée un fichier chiffré avec l'extension .gpg.

7. Déchiffrement d'un fichier​

  1. Sélectionnez le fichier chiffré :
    • Dans l'Explorateur Windows, faites un clic droit sur le fichier chiffré (.gpg).
  2. Déchiffrez le fichier :
    • Dans le menu contextuel, choisissez "Déchiffrer et vérifier".
    • Entrez votre mot de passe (celui que vous avez choisi lors de la création de votre clé privée).
    • Gpg4win déchiffre le fichier et crée une copie déchiffrée.

8. Signature d'un fichier​

  1. Sélectionnez le fichier :
    • Dans l'Explorateur Windows, faites un clic droit sur le fichier que vous souhaitez signer.
  2. Signez le fichier :
    • Dans le menu contextuel, choisissez "Signer et chiffrer".
    • Dans la fenêtre qui s'ouvre, sélectionnez "Signer".
    • Choisissez votre clé privée.
    • Cliquez sur "Suivant", puis sur "Signer".
    • Gpg4win crée un fichier signé (soit un fichier .sig si vous choisissez une signature détachée, soit un fichier .gpg si vous choisissez une signature incluse).

9. Vérification d'une signature​

  • Clic-droit sur le fichier signé -> "Déchiffrer et vérifier".

10. Échangez vous vos clés publiques​

  • Échangez vos clés publiques et essayez de vous envoyer des messages chiffrés et signés.
tip

Ce tutoriel ne couvre que les bases de l'utilisation de Gpg4win. Il existe de nombreuses autres fonctionnalités (gestion des clés, révocation, chiffrement et signature d'emails, etc.). N'hésitez pas à explorer l'interface de Kleopatra et à consulter la documentation de Gpg4win pour en apprendre davantage.

Testez vos connaissances !​

Quel est le but principal des fonctions de hachage et des signatures numériques ?
Qu'est-ce qu'une fonction de hachage cryptographique ?
Quelles sont les propriétés d'une bonne fonction de hachage cryptographique ? (Plusieurs réponses possibles)
Étant donné un hash, est-il facile de retrouver l'entrée originale ?
Est-il facile de trouver des collisions avec une bonne fonction de hachage?
Quelles sont les utilisations courantes des fonctions de hachage ? (Plusieurs réponses possibles)
Parmi les algorithmes suivants, lesquels sont considérés comme obsolètes ou faibles et ne devraient plus être utilisés ? (Plusieurs réponses possibles)
Quelle est la taille du hash produit par SHA-256 ?
Vrai ou Faux: SHA-3 utilise une construction appelée « éponge »
Comment fonctionne la vérification de l'intégrité des données avec une fonction de hachage ?
Quelle attaque peut compromettre la vérification de l'intégrité des données même avec une fonction de hachage forte ?
Quels sont les avantages de la signature numérique ? (Plusieurs réponses possibles)
Comment fonctionne la signature numérique ? (Plusieurs réponses possibles)
Quel algorithme est couramment utilisé pour la signature numérique ?
ECDSA est une variante de DSA qui utilise :